Ornstein-Uhlenbeck kernel

The Laplacian function kernel defines a stationary gaussian process, the Ornstein-Uhlenbeck process:

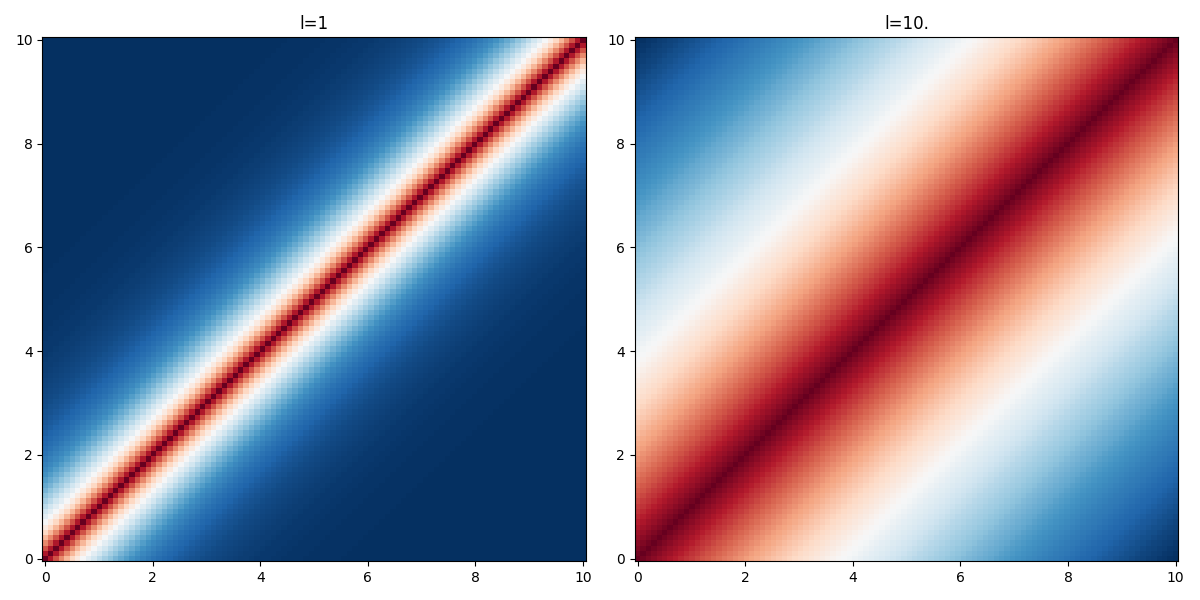
\begin{align*} \displaystyle K(x, x') &= \sigma^2\,\exp\left(-\frac{|d|}{l}\right),\quad d=x'-x \end{align*}

Unlike the Wiener process, this process is mean reverting and admits a stationary probability distribution. It is convenient to model time-series. It can be seen as a noisy relaxation model. (cite:rasmussen2003 p.212)

The parameter \(l\) is the characteristic lengthscale of the process. As one can see on the figure below, the larger the value of \(l\) the "further" the kernel takes non-negligible values.